Kiểm định độc lập Chi bình phương

(Tham khảo chính: thống kê )

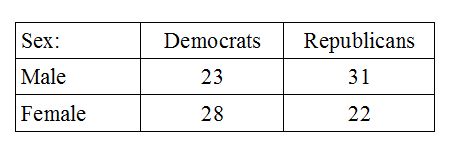
Kiểm định Chi bình phương cũng có thể được sử dụng cho các sơ đồ phân loại phức tạp hơn. Khi thảo luận về lệnh crosstabs, chúng tôi nhận thấy rằng dữ liệu tần số (thang đo danh nghĩa) có thể được phân loại theo hai biến trong một số trường hợp. Ví dụ: chúng ta có thể so sánh tần suất của nam và nữ được xác định là Dân chủ hoặc Cộng hòa. Mỗi người được phân loại theo hai biến để tạo thành bốn nhóm riêng biệt trong ví dụ này: Nam Dân chủ, Nam Cộng hòa, Nữ Dân chủ và Nữ Cộng hòa.

[Hình ảnh minh họa bảng dự phòng này cho thấy hai mức độ giới tính (nam và nữ) và hai mức độ đảng phái chính trị (Dân chủ và Cộng hòa) tạo ra bốn nhóm có thể.]

Trong bối cảnh này, kiểm định Chi bình phương đôi khi được gọi là kiểm định độc lập. Dữ liệu cần được mã hóa để hiển thị tư cách thành viên của mỗi người trong hai biến, như được mô tả cho dữ liệu crosstabs. Dữ liệu có sẵn trong tệp dữ liệu được định dạng crosstabs này.

Đối với Chi bình phương, hãy chạy lệnh crosstabs từ Analyze, Descriptive Statistics, Crosstabs.

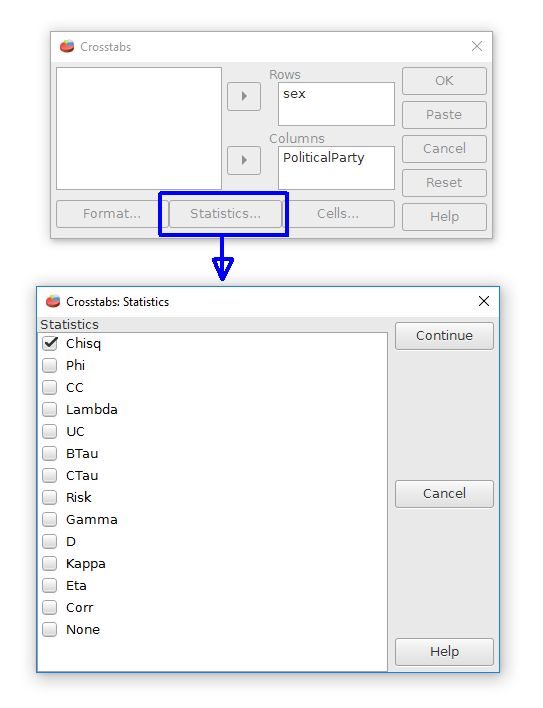
[Hình ảnh minh họa hộp thoại crosstabs với các tùy chọn thống kê.]

Hai biến phân loại khác nhau, Sex và PoliticalParty trong ví dụ này, phải được di chuyển đến các trường hàng hoặc cột.

Nút Statistics từ hộp thoại Crosstabs cho thấy nhiều khả năng kiểm định khác nhau. Kiểm định Chi bình phương được biểu thị là "Chisq". Đánh dấu vào ô này sẽ tạo ra kiểm định Chi bình phương trên các danh mục.

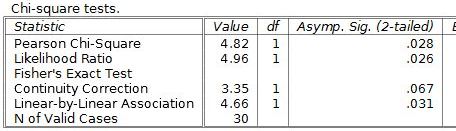
[Hình ảnh minh họa kết quả đầu ra crosstabs hiển thị kết quả kiểm định chi bình phương.]

Hàng Chi bình phương Pearson hiển thị kết quả kiểm định độc lập chi bình phương. Kết quả này sẽ có ý nghĩa thống kê vì nó có giá trị p < 0,05. Các hàng khác đại diện cho các dạng ít được sử dụng hơn của kiểm định chi bình phương.

Theo kiểu APA, kết quả này sẽ được báo cáo là χ2 (bậc tự do, n = cỡ mẫu) = điểm chi bình phương, p = giá trị p. Đối với ví dụ này, nó sẽ là χ2 (1, n = 30) = 4,82, p = 0,028 ở định dạng APA thích hợp.

Tải về tài liệu chính .....(xem tiếp)